变异系数计算公式:了解数据分布的相对离散程度
在统计学中,变异系数(Coefficient of Variation,CV)是一个衡量数据分布相对离散程度的指标。它能够帮助我们比较不同数据集的波动性,即使它们的均值不同。本文将详细介绍变异系数的计算公式、意义以及实际应用。
一、变异系数的定义
变异系数,又称相对标准差,是标准差与均值的比率。标准差是一个绝对指标,反映数据的绝对波动程度,而变异系数是一个相对指标,能够衡量数据的相对波动程度。因此,变异系数在比较不同数据集时更具可比性。
二、变异系数的计算公式
1. 样本变异系数
对于一个样本数据集,样本变异系数的计算公式如下:

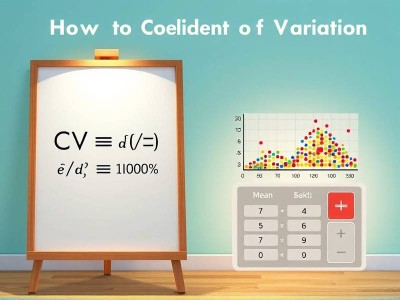
[ CV = \frac{s}{\bar{x}} ]
其中: - ( s ) 为样本标准差 - ( \bar{x} ) 为样本均值
2. 总体变异系数
对于一个总体数据集,总体变异系数的计算公式为:
[ CV = \frac{\sigma}{\mu} ]
其中: - ( \sigma ) 为总体标准差 - ( \mu ) 为总体均值
通常,样本变异系数用于估计总体的变异系数。
三、变异系数的意义
变异系数的重要性在于它能够消除均值大小对数据离散程度度量的影响。由于变异系数是相对指标,因此可以用来比较不同数据集的波动性。例如:
- 如果一个数据集的均值为10,标准差为2,则变异系数为0.2。
- 如果另一个数据集的均值为50,标准差为5,则变异系数为0.1。
虽然第一个数据集的标准差较大,但由于均值较小,其变异系数较小,说明其相对波动程度更小。
四、变异系数的应用
变异系数在多个领域有广泛应用,以下是其主要应用领域:
1. 金融投资
在投资领域,变异系数被用来衡量投资风险与回报之间的关系。变异系数越小,说明单位风险所对应的收益越高;反之,变异系数越大,则说明单位风险所对应的收益较低。
2. 质量控制
在产品质量管理中,变异系数可以用来衡量生产过程的稳定性。变异系数越小,产品质量越稳定;反之,变异系数越大,说明产品质量波动较大。
3. 生物学
在生物学研究中,变异系数被用来比较不同物种或群体的生长速度和变化程度。
4. 社会学
在社会学研究中,变异系数可以用来分析社会现象的稳定性。例如,分析不同地区的人口增长率,变异系数可以帮助我们了解人口增长的波动性。
五、变异系数的计算步骤
-
计算数据集的均值
均值 ( \bar{x} ) 为所有数据之和除以数据的个数 ( n )。 -
计算数据集的标准差
- 计算每个数据与均值的差的平方。
- 计算这些平方差的平均值,即为方差。
-
标准差是方差的平方根。
-
计算变异系数
将标准差除以均值,即得到变异系数。
六、实例分析
实例一:考试成绩的变异系数
假设有两个班级,A班和B班,二年级学生,各50人。A班的成绩均值为70分,标准差为10分;B班的成绩均值为80分,标准差为12分。那么,A班和B班的变异系数分别为:
- A班:( CV_A = \frac{10}{70} \approx 0.1429 )
- B班:( CV_B = \frac{12}{80} = 0.15 )
虽然B班的标准差高于A班,但由于其均值更高,A班的变异系数相对较小,说明A班的成绩更为稳定。
实例二:股票投资的变异系数
假设投资于股票A和股票B,其年均收益率分别为8%和12%,标准差分别为3%和6%。那么,两者的变异系数分别为:
- 股票A:( CV_A = \frac{3}{8} = 0.375 )
- 股票B:( CV_B = \frac{6}{12} = 0.5 )
股票A的变异系数低于股票B,说明在相同的风险水平下,股票A的预期收益更高;而股票B的变异系数更高,说明其波动性更大,适合风险偏好较高的投资者。
七、总结
变异系数是衡量数据相对离散程度的重要指标,能够帮助我们比较不同数据集的波动性。计算公式简单,即标准差与均值的比值。在金融、质量控制、生物学、社会学等多个领域,变异系数都有广泛的应用。了解变异系数的计算方法和意义,有助于我们更深入地分析数据,做出更科学的决策。
通过本篇文章,我们详细介绍了变异系数的计算公式、意义及其应用,并通过实例分析展示了其在实际中的重要性。希望本文能够帮助读者更好地理解和应用这一统计学工具。